代数系统 同态,探索结构映射与代数保真性

你知道吗？在数学的广阔天地里，有一种结构，它就像是一座神秘的城堡，里面充满了各种奇妙的规律。今天，我就要带你走进这座城堡，探索其中的奥秘——代数系统中的同态。

城堡的入口：代数系统

想象你站在一座宏伟的城堡前，这座城堡就是代数系统。它由一群元素和这些元素之间的运算规则组成。比如，我们熟悉的整数加法，就是一个简单的代数系统。在这个系统中，元素是整数，运算是加法。

城堡的走廊：同态

当你走进城堡，你会看到一条条走廊，它们连接着不同的房间。这些走廊就是同态。同态是连接两个代数系统的桥梁，它允许我们在不同的系统之间传递信息和规律。

同态的魔法

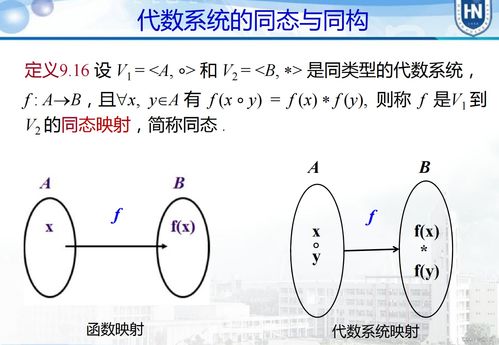
同态有一个神奇的能力，那就是它能够保持运算的规律。比如说，如果你在整数加法系统中有一个运算 a + b = c，那么在另一个代数系统中，通过同态映射，这个运算也会保持不变，即 φ(a) + φ(b) = φ(c)。

城堡的房间：同构

在城堡的深处，有一个特别的地方，那就是同构。同构是同态的一种特殊形式，它不仅能够传递运算规律，还能够保持元素之间的对应关系。简单来说，同构就像是两个完全相同的代数系统，只是它们的名字不同。

同构的奇迹

同构的奇迹在于，它能够让我们看到两个看似完全不同的代数系统之间的内在联系。比如，整数加法系统和模运算系统，虽然它们的元素和运算看起来完全不同，但它们之间却存在着同构。

城堡的守护者：同余关系

在城堡的角落，你还可能会遇到一个神秘的守护者——同余关系。同余关系是一种特殊的等价关系，它能够将代数系统中的元素划分为若干个等价类。这些等价类在运算下保持不变，就像是在城堡中划分出了不同的区域。

同余关系的智慧

同余关系的智慧在于，它能够帮助我们更好地理解代数系统。通过同余关系，我们可以将复杂的代数系统简化为若干个简单的等价类，从而更容易地分析和解决问题。

城堡的探索

当然，这只是代数系统中同态的一小部分。实际上，同态还有许多其他的性质和特点，等待着我们去探索。比如，同态的复合、同态的逆、同态的核等等。

通过今天的探索，你一定对代数系统中的同态有了更深入的了解。这座神秘的城堡，就像数学的海洋一样，充满了无穷的奥秘。希望你能继续探索，发现更多美丽的风景。