典型系统的瞬态响应,典型系统瞬态响应特性解析与应用

你知道吗？在控制系统的世界里，有一个特别神奇的环节，它就像是一个调皮的小精灵，时而活泼跳跃，时而安静沉思。它就是——典型系统的瞬态响应。今天，就让我带你一起探索这个神秘的世界，看看它究竟有哪些奇妙之处吧！

一、初识典型系统

在控制系统的大家庭里，典型系统可是个明星角色。它由比例、惯性、积分、微分等环节组成，就像是一个小小的乐队，每个环节都是乐队中的一员，共同演奏出美妙的音乐。

1. 比例环节：这个环节就像是一个放大器，它把输入信号放大或缩小，但不会改变信号的形状。简单来说，就是一个“放大”的小能手。

2. 惯性环节：这个环节有点像是一个“慢吞吞”的小家伙，它会让信号变得“迟钝”，延迟信号的响应。想象你按下开关，灯泡不会立刻亮起来，而是慢慢变亮，这就是惯性环节的功劳。

3. 积分环节：这个环节就像是一个“记录者”，它会把输入信号的累积值记录下来。简单来说，就是一个“积累”的小助手。

4. 微分环节：这个环节有点像是一个“侦探”，它能够捕捉到信号的微小变化。简单来说，就是一个“敏锐”的小侦探。

二、瞬态响应大揭秘

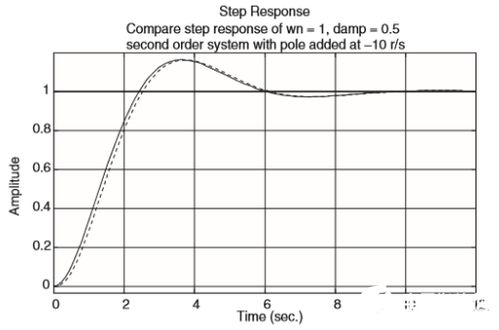
典型系统的瞬态响应，就像是一场精彩的表演。它从初始状态开始，经过一段时间的波动，最终达到稳定状态。这个过程，就像是一个演员从幕后走到台前，逐渐展现出自己的魅力。

1. 上升时间：从输入信号开始，到输出信号达到稳态值的90%所需要的时间。

2. 超调量：输出信号在达到稳态值之前，超过稳态值的最大幅度。

3. 调节时间：从输入信号开始，到输出信号达到稳态值的2%所需要的时间。

4. 稳态误差：输出信号在达到稳态值后，与稳态值之间的差值。

三、稳定性大考验

稳定性是典型系统瞬态响应的关键。一个稳定的系统，就像是一个稳重的舞者，无论遇到多大的挑战，都能保持优雅的姿态。

1. 稳定判据：通过分析系统的传递函数，判断系统是否稳定。

2. 根轨迹：通过绘制根轨迹，分析系统在不同参数下的稳定性。

3. 频率响应：通过分析系统的频率响应，判断系统在不同频率下的稳定性。

四、实例分析

为了更好地理解典型系统的瞬态响应，让我们来看一个实例。

假设我们有一个控制系统，它的传递函数为：

\\[ G(s) = \\frac{K}{(s+1)(s+2)} \\]

其中，K为比例系数。

1. 稳定性分析：通过绘制根轨迹，我们可以发现，当K>0时，系统是稳定的。

2. 瞬态响应分析：通过求解微分方程，我们可以得到系统的瞬态响应曲线。从曲线中，我们可以观察到上升时间、超调量、调节时间和稳态误差等参数。

五、

典型系统的瞬态响应，就像是一个充满魅力的舞台。它既有稳定的舞者，也有调皮的小精灵。通过深入了解和掌握典型系统的瞬态响应，我们可以更好地设计控制系统，让它们在各个领域发挥出巨大的作用。

在这个神奇的世界里，还有许多未知的奥秘等待我们去探索。让我们一起努力，揭开这个世界的神秘面纱，感受典型系统瞬态响应的魅力吧！