代数系统为群,群的定义

代数系统是数学中一个重要的概念，它描述了一组元素及其上的运算。在代数系统中，群是最基本和重要的结构之一。本文将介绍群的定义、性质以及一些常见的群，旨在帮助读者更好地理解群这一代数结构。

群的定义

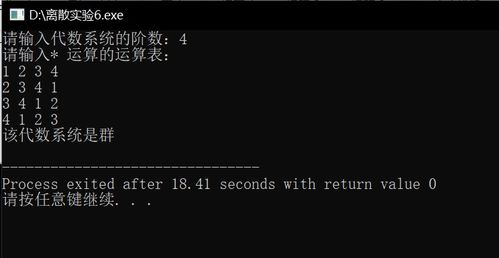
群是一种特殊的代数系统，它由一组元素和一种二元运算组成。具体来说，设 ( G ) 是一个非空集合，( cdot ) 是定义在 ( G ) 上的二元运算，如果 ( G ) 满足以下四个条件，则称 ( G ) 为一个群：

结合律：对于 ( G ) 中的任意三个元素 ( a, b, c )，都有 ( (a cdot b) cdot c = a cdot (b cdot c) )。

存在单位元：存在一个元素 ( e in G )，使得对于 ( G ) 中的任意元素 ( a )，都有 ( a cdot e = e cdot a = a )。

存在逆元：对于 ( G ) 中的任意元素 ( a )，都存在一个元素 ( b in G )，使得 ( a cdot b = b cdot a = e )，其中 ( e ) 是单位元。

封闭性：对于 ( G ) 中的任意两个元素 ( a, b )，都有 ( a cdot b in G )。

群的性质

群具有以下性质：

单位元的唯一性：群中存在唯一的单位元 ( e )，使得对于 ( G ) 中的任意元素 ( a )，都有 ( a cdot e = e cdot a = a )。

逆元的唯一性：群中每个元素 ( a ) 的逆元 ( b ) 是唯一的，使得 ( a cdot b = b cdot a = e )，其中 ( e ) 是单位元。

幂等性：群中每个元素 ( a ) 都满足 ( a cdot a = e )，其中 ( e ) 是单位元。

消去律：对于 ( G ) 中的任意元素 ( a, b, c )，如果 ( a cdot b = a cdot c )，则 ( b = c )；如果 ( b cdot a = c cdot a )，则 ( b = c )。

常见的群

整数加法群：整数集合 ( mathbb{Z} ) 在加法运算下构成一个群，单位元是 0，每个元素的逆元是其相反数。

实数加法群：实数集合 ( mathbb{R} ) 在加法运算下构成一个群，单位元是 0，每个元素的逆元是其相反数。

整数乘法群：非零整数集合 ( mathbb{Z}^ ) 在乘法运算下构成一个群，单位元是 1，每个元素的逆元是其倒数。

实数乘法群：非零实数集合 ( mathbb{R}^ ) 在乘法运算下构成一个群，单位元是 1，每个元素的逆元是其倒数。

置换群：一个有限集合的所有置换构成的集合在复合运算下构成一个群。

结论

群是代数系统中一个重要的概念，它具有丰富的性质和广泛的应用。通过本文的介绍，读者可以了解到群的定义、性质以及一些常见的群。希望本文能够帮助读者更好地理解群这一代数结构。

参考文献

离散数学教材编写组. 离散数学[M]. 北京：高等教育出版社，2018.

张景中. 离散数学[M]. 北京：科学出版社，2015.

丘维声. 离散数学[M]. 北京：清华大学出版社