代数系统同构,代数系统同构概述

代数系统同构概述

代数系统同构是代数学中的一个重要概念，它描述了两个代数系统在结构上的相似性。在数学中，代数系统是由一组元素和在这些元素上定义的运算组成的。同构意味着两个代数系统在运算规则和元素结构上完全相同，只是元素的具体表示可能不同。

代数系统的定义

首先，我们需要明确代数系统的定义。一个代数系统通常由以下三个部分组成：

一个非空集合 ( S )，称为代数系统的元素集。

一个或多个运算，这些运算在元素集 ( S ) 上定义。

运算的封闭性，即对于 ( S ) 中的任意元素 ( a ) 和 ( b )，运算 ( circ ) 在 ( a ) 和 ( b ) 上总是有定义的。

同构的定义

两个代数系统 ( A ) 和 ( B ) 被称为同构的，如果存在一个双射函数 ( f: S_A rightarrow S_B )，使得对于 ( A ) 和 ( B ) 中的任意元素 ( a ) 和 ( b )，以及 ( A ) 和 ( B ) 中的任意运算 ( circ )，都有 ( a circ b = f(a) circ f(b) )。这个函数 ( f ) 被称为同构映射。

同构的性质

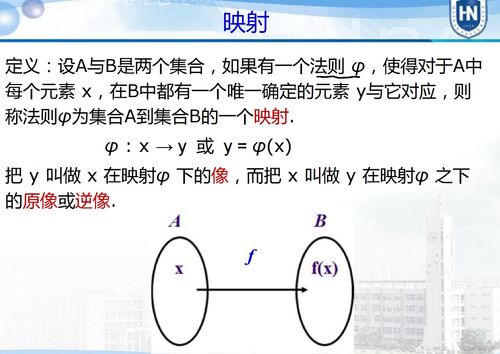
同构映射具有以下性质：

自反性：任何代数系统 ( A ) 都与自身同构。

对称性：如果 ( A ) 和 ( B ) 同构，那么 ( B ) 和 ( A ) 也同构。

传递性：如果 ( A ) 和 ( B ) 同构，( B ) 和 ( C ) 同构，那么 ( A ) 和 ( C ) 也同构。

同构的应用

在群论中，同构用于研究不同群之间的结构相似性。

在环论和域论中，同构用于比较不同环或域的结构。

在计算机科学中，同构用于比较算法和程序的结构相似性。

同构的例子

以下是一个简单的同构例子：

代数系统 ( A )：由集合 ( {0, 1} ) 和运算 ( + )（模 2 加法）组成。

代数系统 ( B )：由集合 ( {a, b} ) 和运算 ( circ )（定义为 ( a circ a = b )，( a circ b = a )，( b circ a = b )，( b circ b = a )）组成。

定义一个同构映射 ( f: A rightarrow B ) 如下：( f(0) = a )，( f(1) = b )。可以验证，对于 ( A ) 和 ( B ) 中的任意元素 ( a ) 和 ( b )，以及运算 ( + ) 和 ( circ )，都有 ( a + b = f(a) circ f(b) )。因此，( A ) 和 ( B ) 是同构的。

结论

代数系统同构是研究代数系统结构相似性的有力工具。通过同构，我们可以比较不同代数系统之间的结构，发现它们之间的内在联系。同构在数学和计算机科学中都有着重要的应用价值。