0系统二阶系统,深入解析二阶系统及其在控制系统中的应用

深入解析二阶系统及其在控制系统中的应用

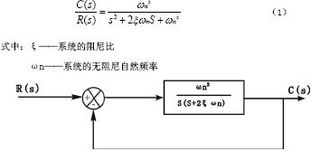
在控制理论中，二阶系统是一个重要的研究对象。它是由二阶线性常微分方程描述的系统，广泛应用于各种工程领域，如电力系统、机械系统、通信系统等。本文将深入解析二阶系统的基本概念、特性以及其在控制系统中的应用。

二阶系统的基本概念

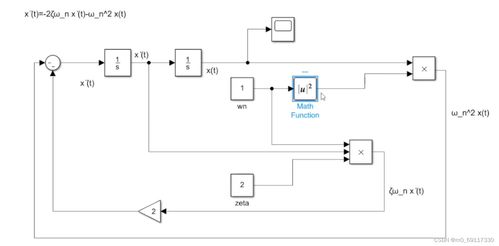
二阶系统是指其数学模型可以表示为二阶线性常微分方程的系统。这类系统的特点是具有两个独立的状态变量，其动态行为可以通过二阶微分方程来描述。二阶系统的数学模型通常可以表示为以下形式：

ddot{x}(t) + a_1dot{x}(t) + a_0x(t) = b_1u(t) + b_0u'(t)

其中，$x(t)$ 是系统的输出，$u(t)$ 是系统的输入，$dot{x}(t)$ 和 $ddot{x}(t)$ 分别是输出的一阶和二阶导数，$a_0$、$a_1$、$b_0$ 和 $b_1$ 是系统参数。

二阶系统的特性

二阶系统的特性主要体现在其阶跃响应上。阶跃响应是指系统在单位阶跃输入下的输出响应。根据系统参数的不同，二阶系统的阶跃响应可以分为以下几种情况：

过阻尼系统：系统响应无振荡，但响应速度较慢。

临界阻尼系统：系统响应无振荡，且响应速度适中。

欠阻尼系统：系统响应有振荡，但最终趋于稳定。

无阻尼系统：系统响应为持续的等幅振荡。

这些特性可以通过系统的阻尼比（$zeta$）和自然频率（$omega_n$）来描述。阻尼比定义为$zeta = frac{c}{2sqrt{mc^2}}$，其中$c$ 是系统的临界阻尼系数，$m$ 是系统的质量。自然频率定义为$omega_n = sqrt{frac{k}{m}}$，其中$k$ 是系统的刚度。

二阶系统在控制系统中的应用

伺服控制系统：二阶系统可以用于描述伺服电机的动态特性，从而设计出高性能的伺服控制系统。

滤波器设计：二阶系统能够实现各种滤波功能，如低通、高通、带通和带阻滤波器。

振动控制：二阶系统可以用于分析机械结构的振动特性，从而设计出有效的振动控制策略。

通信系统：二阶系统可以用于描述通信系统的信道特性，从而设计出高效的调制和解调方案。

在这些应用中，二阶系统的动态特性对于系统的性能至关重要。因此，对二阶系统的分析和设计是控制系统设计中的基础。

二阶系统是控制理论中的一个重要研究对象，其动态特性在各个工程领域都有广泛的应用。通过对二阶系统的深入解析，我们可以更好地理解和设计控制系统，提高系统的性能和稳定性。