4阶系统函数,系统函数的定义

在系统理论中，系统函数是描述系统输入与输出之间关系的重要数学工具。本文将探讨一个4阶系统函数的特性、应用以及如何绘制其零极点分布图、单位冲激响应图和阶跃响应图，同时分析其幅频特性。

系统函数的定义

系统函数H(z)通常表示为系统输入z的拉普拉斯变换与系统输出的拉普拉斯变换的比值。对于一个4阶系统，其系统函数可以表示为：

H(z) = 1 + a1z^(-1) + a2z^(-2) + a3z^(-3) + a4z^(-4)

其中，a1, a2, a3, a4是系统函数的系数，z^(-1), z^(-2), z^(-3), z^(-4)分别代表z的负一次、二次、三次、四次幂。

零极点分布图

零极点分布图是分析系统函数的重要工具，它可以帮助我们了解系统的稳定性和频率响应特性。对于4阶系统函数，我们可以使用MATLAB中的zplane函数来绘制零极点分布图。

以下是一个MATLAB代码示例，用于绘制系统函数H(z)的零极点分布图：

zplane([1, a1, a2, a3, a4]);

通过观察零极点分布图，我们可以判断系统的稳定性。如果所有极点都在单位圆内，则系统是稳定的；如果至少有一个极点在单位圆外，则系统是不稳定的。

单位冲激响应图

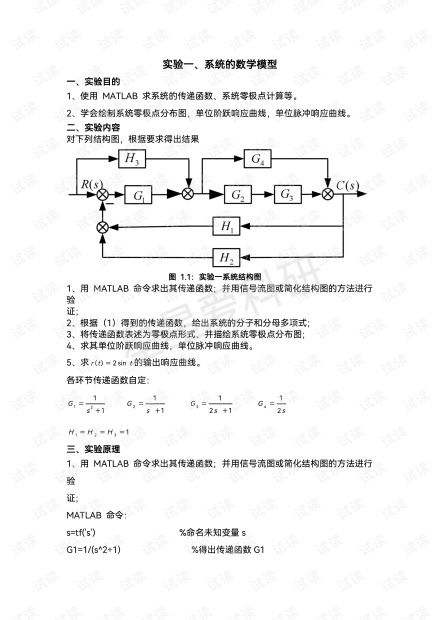
单位冲激响应是系统对单位冲激输入的响应，它反映了系统的动态特性。对于4阶系统函数，我们可以使用MATLAB中的impz函数来绘制单位冲激响应图。

以下是一个MATLAB代码示例，用于绘制系统函数H(z)的单位冲激响应图：

impz([1, a1, a2, a3, a4], 100);

通过观察单位冲激响应图，我们可以了解系统的上升时间、下降时间、超调量和稳态误差等性能指标。

阶跃响应图

阶跃响应是系统对阶跃输入的响应，它反映了系统的稳态性能。对于4阶系统函数，我们可以使用MATLAB中的stepz函数来绘制阶跃响应图。

以下是一个MATLAB代码示例，用于绘制系统函数H(z)的阶跃响应图：

stepz([1, a1, a2, a3, a4], 100);

通过观察阶跃响应图，我们可以了解系统的稳态误差、上升时间、超调量和调节时间等性能指标。

幅频特性

幅频特性描述了系统在不同频率下的增益变化。对于4阶系统函数，我们可以使用MATLAB中的freqs函数来计算幅频特性。

以下是一个MATLAB代码示例，用于计算系统函数H(z)的幅频特性：

[h, w] = freqs([1, a1, a2, a3, a4], logspace(-2, 2, 100));

plot(w, 20log10(abs(h)));

xlabel('Frequency (rad/sample)');

ylabel('Magnitude (dB)');

通过观察幅频特性图，我们可以了解系统在不同频率下的增益变化，从而设计出满足特定性能要求的系统。

结论

本文详细介绍了4阶系统函数的特性、应用以及如何绘制其零极点分布图、单位冲激响应图和阶跃响应图，同时分析了其幅频特性。通过这些分析，我们可以更好地理解系统函数在系统设计中的应用，为实际工程问题提供理论支持。